Sabtu, 13 Oktober 2018

Deteriman matriks metode "Sarrus"

 Assalammualaikum Wr.Wb

Nama saya Dhea Damayanti R (201831007), Saya adalah salah satu mahasiswa di STT-PLN Jakarta.


RESUME
DETERMINAN MATRIKS
“Metode Sarrus”
  Sekolah Tinggi Teknik PLN Jakarta
Dosen : Ibu Evy Yosritas, S,Si.M,Kom
     

Mencari determinan dengan cara Sarrus


A = 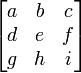\begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i\\ \end{bmatrix} tentukan determinan A
untuk mencari determinan matrik A maka,
detA = (aei + bfg + cdh) - (bdi + afh + ceg)

Metode Sarrus hanya untuk matrix berdimensi 3x3

Menghitung Inverse dari Matrix 3 x 3

A = \begin{bmatrix} 3 & 2 & -1\\ 1 & 6 & 3\\ 2 & -4 & 0\\ \end{bmatrix}
kemudian hitung kofaktor dari matrix A
C11 = 12 C12 = 6 C13 = -16
C21 = 4 C22 = 2 C23 = 16
C31 = 12 C32 = -10 C33 = 16
menjadi matrix kofaktor
\begin{bmatrix} 12 & 6 & -16\\ 4 & 2 & 16\\ 12 & -10 & 16\\ \end{bmatrix}
cari adjoint dari matrix kofaktor tadi dengan mentranspose matrix kofaktor di atas, sehingga menjadi
adj(A) = \begin{bmatrix} 12 & 4 & 12\\ 6 & 2 & -10\\ -16 & 16 & 16\\ \end{bmatrix}
A^{-1} = \frac{1}{det(A)}adj(A)
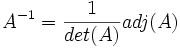
dengan metode Sarrus, kita dapat menghitung determinan dari matrix A
\mathit{det(A) = 64}
A^{-1} = \frac{1}{det(A)}adj(A) = \frac{1}{64} \begin{bmatrix} 12 & 4 & 12\\ 6 & 2 & -10\\ -16 & 16 & 16\\ \end{bmatrix} = \begin{bmatrix} \frac{12}{64} & \frac{4}{64} & \frac{12}{64}\\ \frac{6}{64} & \frac{2}{64} & -\frac{10}{64}\\ -\frac{16}{64} & \frac{16}{64} & \frac{16}{64}\\ \end{bmatrix}

 Sistem Linear Dalam Bentuk Ax = λx

dalam sistem aljabar linear sering ditemukan
      Ax = λx    ; dimana λ adalah skalar
sistem linear tersebut dapat juga ditulis dengan λx-Ax=0, atau dengan memasukkan matrix identitas menjadi
      (λI - A) x = 0
contoh:
diketahui persamaan linear
      x1 + 3x2 = λx1
     4x1 + 2x2 = λx2
dapat ditulis dalam bentuk
     \begin{bmatrix} 1 & 3\\ 4 & 2\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = λ \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix}
yang kemudian dapat diubah
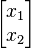
A =\begin{bmatrix} 1 & 3\\ 4 & 2\\ \end{bmatrix}dan x =\begin{bmatrix} x_1\\ x_2\\ \end{bmatrix}
yang kemudian dapat ditulis ulang menjadi
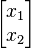
     λ \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} - \begin{bmatrix} 1 & 3\\ 4 & 2\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ \end{bmatrix}

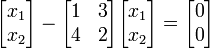
     λ \begin{bmatrix} 1 & 0\\ 0 & 1\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} - \begin{bmatrix} 1 & 3\\ 4 & 2\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ \end{bmatrix}

     \begin{bmatrix} \lambda\,\!-1 & -3\\ -4 & \lambda\,\!-2\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ \end{bmatrix}
sehingga didapat bentuk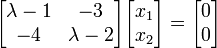
     λ I - A = \begin{bmatrix} \lambda\,\!-1 & -3\\ -4 & \lambda\,\!-2\\ \end{bmatrix}
namun untuk menemukan besar dari λ perlu dilakukan operasi
     det (λ I - A) = 0  ;λ adalah eigenvalue dari A
dan dari contoh diperoleh
     det (λ I - A) = \begin{bmatrix} \lambda\,\!-1 & -3\\ -4 & \lambda\,\!-2\\ \end{bmatrix} = 0
atau λ^2 - 3λ - 10 = 0
dan dari hasil faktorisasi di dapat λ1 = -2 dan λ2 = 5
dengan memasukkan nilai λ pada persamaan (λ I - A) x = 0, maka eigenvector bisa didapat bila λ = -2 maka diperoleh
      \begin{bmatrix} -3 & -3\\ -4 & -4\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ \end{bmatrix}
dengan mengasumsikan x2 = t maka didapat x1 = t
      x = \begin{bmatrix} -t\\ t\\ \end{bmatrix} 
 
Sekian materi singkat yang saya bagikan kepada teman-teman semoga bermanfaat dan dimengerti ya.. SEMANGAT BELAJAR!!! :) 




 
on
Label:

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)