"PERTIDAKSAMAAN" (Kalkulus)

Assalammualaikum Wr.Wb

Nama saya Dhea Damayanti R (201831007), Saya adalah salah satu mahasiswa di STT-PLN Jakarta.
Halaman Blog ini saya buat untuk tugas KALKULUS.

RESUME

"PERTIDAKSAMAAN"

 Sekolah Tinggi Teknik PLN Jakarta

                                                  Dosen : Ibu Evy Yosritas, S,Si.M,Kom.

PERTIDAKSAMAAN :

Pertidaksamaan dalam matematika adalah kalimat/pernyataan matematika yang menunjukkan perbandingan ukuran dua objek atau lebih.
  

Notasi pertidaksamaan:

 

Notasi	Arti	Contoh
<	lebih kecil kurang dari	2 < 3 x + 1 < 3
>	lebih besar lebih dari	3 > 2 3x + 1 > 5
≤	lebih kecil atau sama dengan batas dibawah maksimum maksimal sebanyaknya paling banyak tidak lebih dari sekurangnya	2 ≤ 3 x + 1 ≤ 3
≥	lebih besar atau sama dengan batas diatas minimum minimal sesedikitnya paling sedikit tidak kurang dari selebihnya	3 ≥ 2 3x + 1 ≥ 5
≠	tidak sama dengan	2 ≠ 3 x + 1 ≠ 3
a < x < b	diantara a dan b	2 < x < 5
a ≤ x < b	diantara a dan b bila nilai minimal a	2 ≤ x < 5
a < x ≤ b	diantara a dan b bila maksimal b	2 < x ≤ 5
a ≤ x ≤ b	diantara a dan b bila minimal a dan maksimal b	2 ≤ x ≤ 5

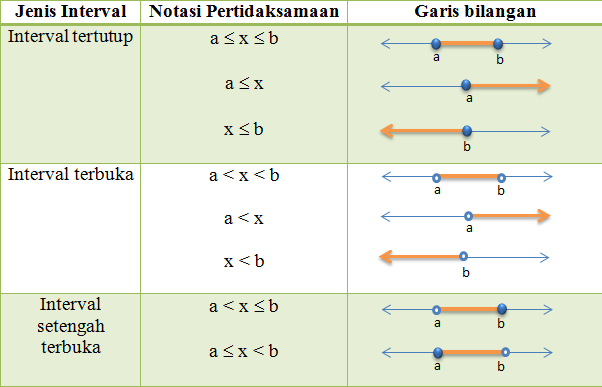
Jenis-jenis pertidaksamaan

Pertidaksamaan Linear

• Tentukan nilai x dari pertidaksamaan ${\displaystyle 6x-7<5x+3}$!

${\displaystyle 6x-7<5x+3}$

${\displaystyle 6x-5x<3+7}$

${\displaystyle x<10}$

${\displaystyle HP=\{x|x<10,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle 5-2x\geq 4x-1}$!

${\displaystyle 5-2x\geq 4x-1}$

${\displaystyle -2x-4x\geq -1-5}$

${\displaystyle -6x\geq -6}$ (karena nilai negatif maka tanda harus terbalik)

${\displaystyle x\leq 1}$

${\displaystyle HP=\{x|x\leq 1,x\in R\}}$

Pertidaksamaan Kuadrat

• Tentukan nilai x dari pertidaksamaan ${\displaystyle x^{2}-7x>10-4x}$!

${\displaystyle x^{2}-7x>10-4x}$

${\displaystyle x^{2}-3x-10>0}$

dibuat harga nol

${\displaystyle x^{2}-3x-10=0}$

${\displaystyle (x+2)(x-5)=0}$

${\displaystyle x=-2\lor x=5}$

dibuat irisan,

${\displaystyle HP=\{x|x<-2\lor x>5,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle 2-x^{2}\leq x-10}$!

${\displaystyle 2-x^{2}\leq x-10}$

${\displaystyle x^{2}+x-12\geq 0}$

dibuat harga nol

${\displaystyle x^{2}+x-12=0}$

${\displaystyle (x+4)(x-3)=0}$

${\displaystyle x=-4\lor x=3}$

dibuat irisan

	(-4)		(3)
+++	N/A	----	N/A	+++

${\displaystyle HP=\{x|x\leq -4\lor x\geq 3,x\in R\}}$

Pertidaksamaan Akar

Dalam bentuk pertidaksamaan akar sebagai berikut:

${\displaystyle {\sqrt {f(x)}}<0}$ atau ${\displaystyle {\sqrt {f(x)}}>0}$

haruslah mempunyai syarat yaitu f(x) ≥ 0.

• Tentukan nilai x dari pertidaksamaan ${\displaystyle {\sqrt {x^{2}-4x}}<{\sqrt {10-x}}}$!

${\displaystyle {\sqrt {x^{2}-4x}}<{\sqrt {10-x}}}$

${\displaystyle ({\sqrt {x^{2}-4x}})^{2}<({\sqrt {10-x}})^{2}}$

${\displaystyle x^{2}-4x<10-x}$

${\displaystyle x^{2}-3x-10<0}$

dibuat harga nol

${\displaystyle x^{2}-3x-10=0}$

${\displaystyle (x+2)(x-5)=0}$

${\displaystyle x=-2\lor x=5}$

dibuat irisan

	-2		5
+++	N/A	----	N/A	+++

${\displaystyle -2<x<5}$

karena ada syarat akar maka:

akar 1

${\displaystyle x^{2}-4x\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-4x=0}$

${\displaystyle x(x-4)=0}$

${\displaystyle x=0\lor x=4}$

dibuat irisan

	0		4
+++	N/A	----	N/A	+++

${\displaystyle x\leq 0\lor x\geq 4}$

akar 2

${\displaystyle 10-x\geq 0}$

${\displaystyle x\leq 10}$

gabungkan umum dan syarat

irisan		-2		(0)		(4)		5		(10)
pertama	tidak	N/A	ya	N/A	ya	N/A	ya	N/A	tidak	N/A	tidak
kedua	ya	N/A	ya	N/A	tidak	N/A	ya	N/A	ya	N/A	ya
ketiga	ya	N/A	ya	N/A	ya	N/A	ya	N/A	ya	N/A	tidak

${\displaystyle HP=\{x|-2<x\leq 0\lor 4\leq x<5,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle {\sqrt {x^{2}-4}}\geq {\sqrt {3x+50}}}$!

${\displaystyle {\sqrt {x^{2}-4}}\geq {\sqrt {3x+50}}}$

${\displaystyle ({\sqrt {x^{2}-4}})^{2}\geq ({\sqrt {3x+50}})^{2}}$

${\displaystyle x^{2}-4\geq 3x+50}$

${\displaystyle x^{2}-3x-54\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-3x-54=0}$

${\displaystyle (x+6)(x-9)=0}$

${\displaystyle x=-6\lor x=9}$

dibuat irisan

	(-6)		(9)
+++	N/A	----	N/A	+++

${\displaystyle x\leq -6\lor x\geq 9}$

karena ada syarat akar maka:

akar 1

${\displaystyle x^{2}-4\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-4=0}$

${\displaystyle (x+2)(x-2)=0}$

${\displaystyle x=-2\lor x=2}$

dibuat irisan

	(-2)		(2)
+++	N/A	----	N/A	+++

${\displaystyle x\leq -2\lor x\geq 2}$

akar 2

${\displaystyle 3x+50\geq 0}$

${\displaystyle x\geq -{\frac {50}{3}}}$

gabungkan umum dan syarat

irisan		(-50/3)		(-6)		(-2)		(2)		(9)
pertama	ya	N/A	ya	N/A	tidak	N/A	tidak	N/A	tidak	N/A	ya
kedua	ya	N/A	ya	N/A	ya	N/A	tidak	N/A	ya	N/A	ya
ketiga	tidak	N/A	ya	N/A	ya	N/A	ya	N/A	ya	N/A	ya

${\displaystyle HP=\{x|2<x\leq 0\lor 4\leq x<5,x\in R\}}$

Pertidaksamaan Pecahan

Dalam bentuk pertidaksamaan pecahan sebagai berikut:

${\displaystyle {\frac {f(x)}{g(x)}}<0}$ atau ${\displaystyle {\frac {f(x)}{g(x)}}>0}$

haruslah mempunyai syarat yaitu penyebut atau g(x) ≠ 0.

• Tentukan nilai x dari pertidaksamaan ${\displaystyle {\frac {x-4}{x-3}}<{\frac {x+1}{x-2}}}$!

${\displaystyle {\frac {x-4}{x-3}}<{\frac {x+1}{x-2}}}$

${\displaystyle {\frac {x-4}{x-3}}-{\frac {x+1}{x-2}}<0}$

${\displaystyle {\frac {(x-4)(x-2)-(x+1)(x-3)}{(x-3)(x-2)}}<0}$

${\displaystyle {\frac {(x^{2}-6x+8)-(x^{2}-2x-3)}{(x-3)(x-2)}}<0}$

${\displaystyle {\frac {-4x+11}{(x-3)(x-2)}}<0}$

${\displaystyle -4x+11<0}$

${\displaystyle x<{\frac {11}{4}}}$

karena ada syarat pecahan maka:

penyebut 1

${\displaystyle x-3\neq 0}$

${\displaystyle x\neq 3}$

penyebut 2

${\displaystyle x-2\neq 0}$

${\displaystyle x\neq 2}$

dibuat irisan

	2		11/4		3
+++	N/A	----	N/A	+++	N/A	----

${\displaystyle HP=\{x|2<x<{\frac {11}{4}}\lor x>3,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle {\frac {x+6}{x+17}}\geq {\frac {1}{x-3}}}$!

${\displaystyle {\frac {x+6}{x+17}}\geq {\frac {1}{x-3}}}$

${\displaystyle {\frac {x+6}{x+17}}-{\frac {1}{x-3}}\geq 0}$

${\displaystyle {\frac {(x+6)(x-3)-(x+17)}{(x+17)(x-3)}}\geq 0}$

${\displaystyle {\frac {x^{2}+3x-18-x-17}{(x+17)(x-3)}}\geq 0}$

${\displaystyle {\frac {x^{2}+2x-35}{(x-3)(x-2)}}\geq 0}$

${\displaystyle x^{2}+2x-35\geq 0}$

dibuat harga nol

${\displaystyle x^{2}+2x-35=0}$

${\displaystyle (x+7)(x-5)=0}$

${\displaystyle x=-7\lor x=5}$ (tanpa gambar irisan)

karena ada syarat pecahan maka:

penyebut 1

${\displaystyle x+17\neq 0}$

${\displaystyle x\neq -17}$

penyebut 2

${\displaystyle x-3\neq 0}$

${\displaystyle x\neq 3}$

dibuat irisan

	-17		(-7)		3		(5)
+++	N/A	----	N/A	+++	N/A	----	N/A	+++

${\displaystyle HP=\{x|x<-17\lor -7\leq x<3\lor x\geq 5,x\in R\}}$

Pertidaksamaan Mutlak

Dalam bentuk pertidaksamaan mutlak sebagai berikut:

${\displaystyle |f(x)|<g(x)}$ atau ${\displaystyle |f(x)|>g(x)}$

haruslah mempunyai dua nilai yaitu

${\displaystyle |f(x)|=\left\{{\begin{matrix}|f(x)|<g(x),&{\mbox{maka penyelesaian}}-g(x)<f(x)<g(x)\\\\|f(x)|>g(x),&{\mbox{maka penyelesaian}}f(x)<-g(x)\lor f(x)>g(x)\end{matrix}}\right.}$

Pertidaksamaan mutlak akan memungkinkan definit + dan - karena tidak memotong dan menyinggung sumbu y.

• Tentukan nilai x dari pertidaksamaan ${\displaystyle |x^{2}+x|<12}$!

${\displaystyle |x^{2}+x|<12}$

karena f(x) < g(x) maka penyelesaian -g(x) < f(x) < g(x)

${\displaystyle -12<x^{2}+x<12}$

untuk ${\displaystyle -12<x^{2}+x}$

${\displaystyle -12<x^{2}+x}$

${\displaystyle x^{2}+x+12>0}$ definit +

untuk ${\displaystyle x^{2}+x<12}$

${\displaystyle x^{2}+x<12}$

${\displaystyle x^{2}+x-12<0}$

dibuat harga nol

${\displaystyle x^{2}+x-12=0}$

${\displaystyle (x+4)(x-3)<0}$

${\displaystyle x=-4\lor x=3}$

dibuat irisan

	-4		3
+++	N/A	----	N/A	+++

${\displaystyle -4<x<3}$

${\displaystyle HP=\{x|-4<x<3,x\in R\}}$

• Tentukan nilai x dari persamaan ${\displaystyle |x^{2}-4x-12|-|7-6x|\geq 5}$!

terlebih dahulu untuk mempunyai batas-batas yang ada

untuk | x^2 - 4x - 12 |

${\displaystyle |x^{2}-4x-12|=\left\{{\begin{matrix}x^{2}-4x-12,&{\mbox{maka penyelesaian}}x^{2}-4x-12\geq 0\\\\-(x^{2}-4x-12),&{\mbox{maka penyelesaian}}x^{2}-4x-12<0\end{matrix}}\right.}$

batasan f(x)

${\displaystyle x^{2}-4x-12\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-4x-12=0}$

${\displaystyle (x+2)(x-6)=0}$

${\displaystyle x=-2\lor x=6}$

dibuat irisan

	-2		6
+++	N/A	----	N/A	+++

${\displaystyle x\leq -2\lor x\geq 6}$

batasan -f(x)

${\displaystyle x^{2}-4x-12<0}$

dibuat harga nol

${\displaystyle x^{2}-4x-12=0}$

${\displaystyle (x+2)(x-6)=0}$

${\displaystyle x=-2\lor x=6}$

dibuat irisan

	-2		6
+++	N/A	----	N/A	+++

${\displaystyle -2<x<6}$

untuk | 7 - 6x |

${\displaystyle |7-6x|=\left\{{\begin{matrix}7-6x,&{\mbox{maka penyelesaian}}7-6x\geq 0\\\\-(7-6x),&{\mbox{maka penyelesaian}}7-6x<0\end{matrix}}\right.}$

batasan f(x)

${\displaystyle 7-6x\geq 0}$

${\displaystyle x\leq {\frac {7}{6}}}$

batasan -f(x)

${\displaystyle 7-6x<0}$

${\displaystyle x>{\frac {7}{6}}}$

keempat batas-batas akan dibuat irisan

irisan		-2		7/6		6
pertama	x^2 - 4x - 12	N/A		N/A		N/A	x^2 - 4x - 12
kedua		N/A	-(x^2 - 4x - 12)	N/A	-(x^2 - 4x - 12)	N/A
ketiga	7 - 6x	N/A	7 - 6x	N/A		N/A
keempat		N/A		N/A	-(7 - 6x)	N/A	-(7 - 6x)

untuk x <= -2

${\displaystyle x^{2}-4x-12-(7-6x)\geq 5}$

${\displaystyle x^{2}-4x-12-7+6x-5\geq 0}$

${\displaystyle x^{2}+2x-24\geq 0}$

dibuat harga nol

${\displaystyle x^{2}+2x-24=0}$

${\displaystyle (x+6)(x-4)=0}$

${\displaystyle x=-6\lor x=4}$

dibuat irisan

	(-6)		(-2)		(4)
Ya	N/A	Ya	N/A	Tidak	N/A	Tidak
+++	N/A	----	N/A	----	N/A	+++

${\displaystyle x\leq -6}$

untuk -2 < x <= 7/6

${\displaystyle -(x^{2}-4x-12)-(7-6x)\geq 5}$

${\displaystyle -x^{2}+4x+12-7+6x-5\geq 0}$

${\displaystyle x^{2}-10x\leq 0}$

dibuat harga nol

${\displaystyle x^{2}-10x=0}$

${\displaystyle x(x-10)=0}$

${\displaystyle x=0\lor x=10}$

dibuat irisan

	-2		(0)		(7/6)		(10)
Tidak	N/A	Ya	N/A	Ya	N/A	Tidak	N/A	Tidak
+++	N/A	+++	N/A	----	N/A	----	N/A	+++

${\displaystyle 0\leq x\leq {\frac {7}{6}}}$

untuk 7/6 < x < 6

${\displaystyle -(x^{2}-4x-12)-(-(7-6x))\geq 5}$

${\displaystyle -x^{2}+4x+12+7-6x-5\geq 0}$

${\displaystyle x^{2}+2x\leq 0}$

dibuat harga nol

${\displaystyle x^{2}+2x=0}$

${\displaystyle x(x+2)=0}$

${\displaystyle x=0\lor x=-2}$

dibuat irisan

	(-2)		(0)		7/6		6
Tidak	N/A	Tidak	N/A	Tidak	N/A	Ya	N/A	Tidak
+++	N/A	----	N/A	+++	N/A	+++	N/A	+++

${\displaystyle \varnothing }$

untuk x >= 6

${\displaystyle x^{2}-4x-12-(-(7-6x))\geq 5}$

${\displaystyle x^{2}-4x-12+7-6x-5\geq 0}$

${\displaystyle x^{2}-10x-10\geq 0}$ definit +

${\displaystyle \varnothing }$

${\displaystyle HP=\{x|x\leq -6\lor 0\leq x\leq {\frac {7}{6}},x\in R\}}$

gabungkan ketiga batas-batas. jadi:

${\displaystyle HP=\{x|-{\frac {11}{5}}\leq x<-{\frac {4}{3}}\lor -{\frac {4}{3}}\leq x\leq 3,x\in R\}}$

${\displaystyle HP=\{x|-{\frac {11}{5}}\leq x\leq 3,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle |{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|}$!

${\displaystyle |{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|}$

${\displaystyle ({\frac {x+4}{10-x}})^{2}<({\frac {1}{x-2}})^{2}}$

${\displaystyle ({\frac {x+4}{10-x}})^{2}-({\frac {1}{x-2}})^{2}<0}$

${\displaystyle ({\frac {x+4}{10-x}}+{\frac {1}{x-2}})({\frac {x+4}{10-x}}-{\frac {1}{x-2}})<0}$

${\displaystyle ({\frac {(x+4)(x-2)+10-x}{(10-x)(x-2)}})({\frac {(x+4)(x-2)-(10-x)}{(10-x)(x-2)}})<0}$

${\displaystyle ({\frac {x^{2}+2x-8+10-x}{(10-x)(x-2)}})({\frac {x^{2}+2x-8-10+x}{(10-x)(x-2)}})<0}$

${\displaystyle ({\frac {x^{2}+x+2}{(10-x)(x-2)}})({\frac {x^{2}+3x-18}{(10-x)(x-2)}})<0}$

akar dari ${\displaystyle {\frac {x^{2}+x+2}{(10-x)(x-2)}}}$

${\displaystyle {\frac {x^{2}+x+2}{(10-x)(x-2)}}<0}$

${\displaystyle x^{2}+x+2=0}$ definit +

karena ada syarat pecahan maka:

penyebut 1

${\displaystyle 10-x\neq 0}$

${\displaystyle x\neq 10}$

penyebut 2

${\displaystyle x-2\neq 0}$

${\displaystyle x\neq 2}$

akar dari ${\displaystyle {\frac {x^{2}+3x-18}{(10-x)(x-2)}}}$

${\displaystyle {\frac {x^{2}+3x-18}{(10-x)(x-2)}}<0}$

${\displaystyle x^{2}+3x-18<0}$

dibuat harga nol

${\displaystyle x^{2}+3x-18=0}$

${\displaystyle (x+6)(x-3)=0}$

${\displaystyle x=-6\lor x=3}$ (tanpa gambar irisan)

karena ada syarat pecahan maka:

penyebut 1

${\displaystyle 10-x\neq 0}$

${\displaystyle x\neq 10}$

penyebut 2

${\displaystyle x-2\neq 0}$

${\displaystyle x\neq 2}$

dibuat irisan

	-6		2*		3		10*
+++	N/A	----	N/A	----	N/A	+++	N/A	+++

nb: * = mempunyai 2 akar

${\displaystyle HP=\{x|-6<x<3,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle |{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|}$!

${\displaystyle |{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|}$

${\displaystyle ({\sqrt {x^{2}-4x}})^{2}\geq ({\sqrt {3x-10}})^{2}}$

${\displaystyle x^{2}-4x\geq 3x-10}$

${\displaystyle x^{2}-7x+10\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-7x+10=0}$

${\displaystyle (x-2)(x-5)=0}$

${\displaystyle x=2\lor x=5}$

dibuat irisan

	2		5
+++	N/A	----	N/A	+++

${\displaystyle x\leq 2\lor x\geq 5}$

karena ada syarat akar maka:

akar 1

${\displaystyle x^{2}-4x\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-4x=0}$

${\displaystyle x(x-4)=0}$

${\displaystyle x=0\lor x=4}$

dibuat irisan

	0		4
+++	N/A	----	N/A	+++

${\displaystyle x\leq 0\lor x\geq 4}$

akar 2

${\displaystyle 3x-10\geq 0}$

${\displaystyle x\geq {\frac {10}{3}}}$

gabungkan umum dan syarat

irisan		(0)		(2)		(10/3)		(4)		(5)
pertama	ya	N/A	ya	N/A	tidak	N/A	tidak	N/A	tidak	N/A	ya
kedua	ya	N/A	tidak	N/A	tidak	N/A	tidak	N/A	ya	N/A	ya
ketiga	tidak	N/A	tidak	N/A	tidak	N/A	ya	N/A	ya	N/A	ya

${\displaystyle HP=\{x|x\geq 5,x\in R\}}$

	-2		5
+++	N/A	----	N/A	+++