"Grafik Fungsi" (Kalkulus)

Assalammualaikum Wr.Wb

Nama saya Dhea Damayanti R (201831007), Saya adalah salah satu mahasiswa di STT-PLN Jakarta.
Halaman Blog ini saya buat untuk tugas KALKULUS.

RESUME

"Grafik fungsi"

 Sekolah Tinggi Teknik PLN Jakarta

                                                  Dosen : Ibu Evy Yosritas, S,Si.M,Kom.

   

Fungsi dan Grafiknya

Definisi   
sebuah fungsi f adaIah suatu aturan korespondensi yang menghubungkan tiap obyek x dalam satu himpunan, yang disebut daerah asal (domain), dengan sebuah nilai tunggal f(x) dari suatu himpunan kedua. Himpunan nilal yang diperoleh secara
demikian disebut daerah hasil (range) fungsi.


Daerah asal dan daerah hasil untuk fungsi f dan g, diperlihatkan dalam tabel berikut.

Macam-Macam Fungsi

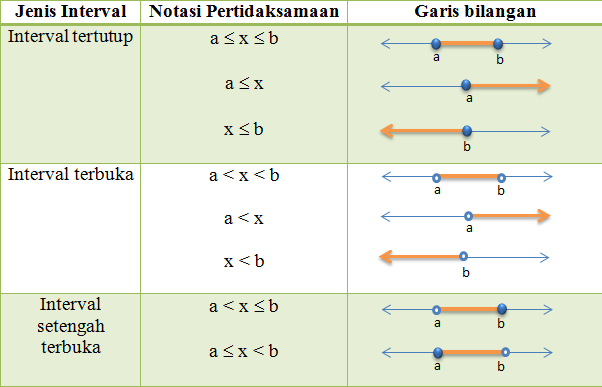
1. Fungsi tangga (bertingkat)

Suatu fungsi f(x) disebut fungsi tangga apabila grafik fungsi f(x) berbentuk

interval-interval yang sejajar.

3. Fungsi ganjil dan fungsi genap

Suatu fungsi f(x) disebut fungsi ganjil apabila berlaku f(–x) = –f(x) dan disebut

fungsi genap apabila berlaku f(–x) = f(x). Jika f(–x) ≠ –f(x) maka fungsi ini

tidak genap dan tidak ganjil.

4.) Fungsi kuadrat

Suatu fungsi f(x) disebut fungsi kuadrat apabila fungsi itu ditentukan oleh

f(x) = ax2 + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan dan

grafiknya berupa parabola

5.) Fungsi Polinomial

Fungsi Polinomial adalah fungsi f yang dinyatakan dalam bentuk :

f(x) = an x n + an-1 x n-1 + ……. A2 x 2 + a1 x a0

Jika n = 1 maka terbentuk fungsi linier (grafiknya berbentuk garis lurus).

Jika n = 2 maka terbentuk fungsi kuadrat( grafiknya berbentuk parabola).

6.) Fungsi modulus

Suatu fungsi f(x) disebut fungsi modulus (mutlak) apabila fungsi ini memetakan

setiap bilangan real pada domain fungsi ke unsur harga mutlaknya.

7..) Fungsi logaritma

Fungsi ini berperan pada persoalan-2 statistik dan probabilitas. Dan lebih banyak kepada persoalan-2 diskrit. Contoh: bagaimana mengatur agar antrian pembelian bensin sedemikian sehingga pada saat-2 tertentu pegawai pelayanan diperbanyak. Misal pada pembayaran rekening listrik, para konsumen lebih banyak membayar pada akhir tagihan daripada awal-awal penagihan. Sangat bijak manajer mengatur agar pada hari-2 terakhir pegawainya hrus membantuk bagian kasir untuk melayani konsumen.

Operasi pada Fungsi

Jika f dan g dua fungsi maka jumlah f + g, selisih f – g, hasil kali fg, hasil bagi
f/g dan perpangkatan fn adalah fungsi-fungsi dengan daerah asal berupa irisan dari
daerah asal f dan daerah asal g, dan dirumuskan sebagai berikut.

(f + g)(x) = f (x) + g(x)
(f – g)(x) = f (x) – g(x)
(f g)(x) = f (x) g(x)
(f / g)(x) = f (x) / g(x) asalkan g(x) ≠ 0

Selanjutnya didefinisikan komposisi fungsi sebagai berikut.

Jika f dan g dua fungsi dengan daerah asal g merupakan daerah hasil f maka
komposisi g o f memenuhi
(g o f)(x) = g (f(x))


Contoh

Jika f(x) = x2 – 2x dan g(x) = x – 1, tentukan g o f dan f o g.

Penyelesaian:
(g o f)(x) = g (f(x))
= g (x2 – 2x)
= x2 – 2x – 1

(f o g)(x) = f (g(x))
= f (x – 1)
= (x – 1)2 – 2(x – 1)
= x2 – 2x + 1 – 2x + 2
= x2 – 4x + 3

 

"Harga Mutlak" (Kalkulus)

Assalammualaikum Wr.Wb

Nama saya Dhea Damayanti R (201831007), Saya adalah salah satu mahasiswa di STT-PLN Jakarta.
Halaman Blog ini saya buat untuk tugas KALKULUS.

RESUME

"Harga Mutlak"

 Sekolah Tinggi Teknik PLN Jakarta

                                                  Dosen : Ibu Evy Yosritas, S,Si.M,Kom.

Menyelesaikan Persamaan dan Pertidaksamaan Harga Mutlak

Menyelesaikan Persamaan Mutlak

 Harga Mutlak suatu bilangan dapat diartikan jarak antara bilangan tersebut dari titik nol(0). Dengan demikian jarak selalu bernilai positif.
Misalnya:
Parhatikan garis bilangan berikut.


Jarak angka 6 dari titik 0 adalah 6
Jarak angka -6 dari titik 0 adalah 6 
jarak angka -3 dari titik 0 adalah 3
Jarak angka 3 dari titik0 adalah 3.

Dari penjelesan di atas memang tampak bahwa nilai mutlak suatu bilangan selalu bernilai positif. 
Berkaitan dengan menentukan nilai mutlak suatu bilangan, maka muncullah tanda mutlak. Tanda mutlak disimbolkan dengan  garis 2 ditepi suatu bilangan atau bentuk aljabar.
Misalnya seperti berikut.

Secara umum, bentuk persamaan nilai mutlak dapat dimaknai seperti berikut.

Jika kita mempunyai persamaan dalam bentuk aljabar, maka dapat dimaknai sebagai berikut.

Jadi, bentuk dasar di atas dpat digunakan untuk membantu menyelesaikan persamaan mutlak.
Lebih jelasnya perhatikan contoh-contoh berikut.

Contoh
Tentukan himpunan penyelesaian dari persamaan nilai Mutlak di bawah ini.

Jawaban:
Bentuk-Bentuk persamaan nilai mutlak di atas dapat diselesaikan sebagai berikut. Pada prinsipnya, langkah langkah penyelesaian nilai mutlak diusahakan bentuk mutlak berada di ruas kiri. 
1. Pada bentuk ini ada dua penyelesaian.
   (*) x + 5 = 3  , maka  x = 3 - 5 = -2
   (**) x + 5 = -3, maka x = -3 - 5 = -8
  Jadi, himpunan penyelesaiannya adalah {-2, -8}

2.  Pada bentuk ini ada dua penyelesaian.
   (*) 2x + 3 = 5  , maka  2x = 5 - 3
                                       2x = 2  <==>  x = 1
   (**) 2x + 3 = -5  , maka  2x = -5 -3
                                         2x = -8  <==> x = -4
  Jadi, himpunan penyelesaiannya adalah {-4, 1}

3. Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu x+1. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan x+1>= 0 atau x >= -1

Bagian kedua untuk batasan x+1< 0 atau x < -1
Mari kita selesaikan.
(*) untuk x >=-1
     Persamaan mutlak dapat ditulis:
    (x + 1) + 2x = 7
                   3x = 7 - 1
                   3x = 6
                     x = 2 (terpenuhi, karena batasan >= -1)

(**) untuk x < -1
     Persamaan mutlak dapat ditulis:
    -(x + 1) + 2x = 7
        -x - 1 + 2x = 7
                      x = 7 + 1                
                      x = 8 (tidak terpenuhi, karena batasan < -1)

Jadi, Himpunan penyelesaiannya adalah {2}.

 4. 
Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu 3x + 4. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan 3x+4>= 0 atau x >= -4/3

Bagian kedua untuk batasan 3x+4< 0 atau x < -4/3
Mari kita selesaikan.
(*) untuk x >=-4/3
     Persamaan mutlak dapat ditulis:
    (3x + 4) = x - 8
        3x - x = -8 - 4
             2x =-12
               x = -6 (tidak terpenuhi, karena batasan >= -4/3)
(**) untuk x < -4/3
     Persamaan mutlak dapat ditulis:
    -(3x + 4) = x - 8
        -3x - 4 = x -8
         -3x - x = -8 + 4
              -4x = -4
                 x = 1 (tidak terpenuhi, karena batasan < -4/3)

Jadi, Tidak ada Himpunan penyelesaiannya.

Menyelesaikan Pertidaksamaan Nilai Mutlak
Menyelesaikan pertidaksamaan nilai mutlak caranya hampir sama dengan persamaan nilai mutlak. hanya saja berbeda sedikit pada tanda ketidaksamaannya. Langkah-langkah selanjutnya seperti menyelesaikan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan  mutlak dapat digambarkan sebagai berikut.

Apabila fungsi di dalam nilai mutlak berbentuk ax + b maka pertidaksamaan nilai mutlak dapat diselesaikan seperti berikut.








Lebih jelasnya perhatikan contoh berikut ini.

Contoh
Tentukan himpunan penyelesaian dari Pertidaksamaan nilai mutlak berikut ini.

Jawaban
1. Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
    -9 < x+7 < 9
    -9 - 7 < x < 9 - 7
       -16 < x < 2
   Jadi, himpunan penyelesaiannya adalah { x/ -16 < x < 2}

2. Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua bagian.
   (*) 2x - 1 >=  7
             2x  >=  7 + 1
             2x  >= 8
               x  >= 4

  (**) 2x - 1 <= -7
             2x   <= -7 + 1
             2x   <= -6
               x   <= -3
  
    Jadi, himpunan penyelesaiannya adalah { x/ x <= -3 atau x >= 4}

 3. Kalau dalam bentuk soal ini, langkah menyelesaikan pertidaksamaannya dengan mengkuadratkan kedua ruas.
perhatikan proses berikut ini.

(x + 3)² <= (2x – 3)²

(x + 3)² - (2x – 3)² <= 0

(x + 3 + 2x – 3) - (x + 3 – 2x + 3) <= 0 (ingat: a² – b² = (a+b)(a-b))

x (6 - x) <=0

Pembuat nol adalah x = 0 dan x = 6

Mari selidiki menggunakan garis bilangan

Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.

Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.

Mari selidiki menggunakan garis bilangan

Oleh karena batasnya <= 0, maka penyelesaiannya adalah x <=0 atau x >=6.

Jadi, himpunan penyelesaiannya adalah {x/ x <= 0 atau x >= 6}.

4. Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih mudah menggunakan cara menjabarkan definisi.
Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.

Dari batasan batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.

Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3  ......(1)
   (3x + 1) - (2x + 4) < 10
          3x + 1 - 2x- 4 < 10
                         x- 3 < 10
                             x < 13 .......(2)

  Dari (1) dan (2) diperoleh irisan penyelesaian -1/3 <= x < 13

2. Untuk batasan -2<= x < -1/3  ......(1)
    -(3x + 1) - (2x + 4) < 10
          -3x - 1 - 2x - 4 < 10
                       -5x - 5 < 10
                             -5x < 15 
                               -x < 3
                             x > 3 .......(2)

  Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada penyelesaian.

3. Untuk batasan x < -2  ......(1)
   -(3x + 1) + (2x + 4) < 10
         -3x - 1 + 2x + 4 < 10
                        -x + 3 < 10
                             -x  < 7
                                x > -7 .......(2)

  Dari (1) dan (2) diperoleh irisan penyelesaian -7 < x < -2.

Jadi, himpunan penyelesaiannya adalah {x/ -1/3 <= x < 13 atau -7 < x < -2}.

Perhatikan contoh Pertidaksamaan mutlak lainnya berikut.

"PERTIDAKSAMAAN" (Kalkulus)

Assalammualaikum Wr.Wb

Nama saya Dhea Damayanti R (201831007), Saya adalah salah satu mahasiswa di STT-PLN Jakarta.
Halaman Blog ini saya buat untuk tugas KALKULUS.

RESUME

"PERTIDAKSAMAAN"

 Sekolah Tinggi Teknik PLN Jakarta

                                                  Dosen : Ibu Evy Yosritas, S,Si.M,Kom.

PERTIDAKSAMAAN :

Pertidaksamaan dalam matematika adalah kalimat/pernyataan matematika yang menunjukkan perbandingan ukuran dua objek atau lebih.
  

Notasi pertidaksamaan:

 

Notasi	Arti	Contoh
<	lebih kecil kurang dari	2 < 3 x + 1 < 3
>	lebih besar lebih dari	3 > 2 3x + 1 > 5
≤	lebih kecil atau sama dengan batas dibawah maksimum maksimal sebanyaknya paling banyak tidak lebih dari sekurangnya	2 ≤ 3 x + 1 ≤ 3
≥	lebih besar atau sama dengan batas diatas minimum minimal sesedikitnya paling sedikit tidak kurang dari selebihnya	3 ≥ 2 3x + 1 ≥ 5
≠	tidak sama dengan	2 ≠ 3 x + 1 ≠ 3
a < x < b	diantara a dan b	2 < x < 5
a ≤ x < b	diantara a dan b bila nilai minimal a	2 ≤ x < 5
a < x ≤ b	diantara a dan b bila maksimal b	2 < x ≤ 5
a ≤ x ≤ b	diantara a dan b bila minimal a dan maksimal b	2 ≤ x ≤ 5

Jenis-jenis pertidaksamaan

Pertidaksamaan Linear

• Tentukan nilai x dari pertidaksamaan ${\displaystyle 6x-7<5x+3}$!

${\displaystyle 6x-7<5x+3}$

${\displaystyle 6x-5x<3+7}$

${\displaystyle x<10}$

${\displaystyle HP=\{x|x<10,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle 5-2x\geq 4x-1}$!

${\displaystyle 5-2x\geq 4x-1}$

${\displaystyle -2x-4x\geq -1-5}$

${\displaystyle -6x\geq -6}$ (karena nilai negatif maka tanda harus terbalik)

${\displaystyle x\leq 1}$

${\displaystyle HP=\{x|x\leq 1,x\in R\}}$

Pertidaksamaan Kuadrat

• Tentukan nilai x dari pertidaksamaan ${\displaystyle x^{2}-7x>10-4x}$!

${\displaystyle x^{2}-7x>10-4x}$

${\displaystyle x^{2}-3x-10>0}$

dibuat harga nol

${\displaystyle x^{2}-3x-10=0}$

${\displaystyle (x+2)(x-5)=0}$

${\displaystyle x=-2\lor x=5}$

dibuat irisan,

${\displaystyle HP=\{x|x<-2\lor x>5,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle 2-x^{2}\leq x-10}$!

${\displaystyle 2-x^{2}\leq x-10}$

${\displaystyle x^{2}+x-12\geq 0}$

dibuat harga nol

${\displaystyle x^{2}+x-12=0}$

${\displaystyle (x+4)(x-3)=0}$

${\displaystyle x=-4\lor x=3}$

dibuat irisan

	(-4)		(3)
+++	N/A	----	N/A	+++

${\displaystyle HP=\{x|x\leq -4\lor x\geq 3,x\in R\}}$

Pertidaksamaan Akar

Dalam bentuk pertidaksamaan akar sebagai berikut:

${\displaystyle {\sqrt {f(x)}}<0}$ atau ${\displaystyle {\sqrt {f(x)}}>0}$

haruslah mempunyai syarat yaitu f(x) ≥ 0.

• Tentukan nilai x dari pertidaksamaan ${\displaystyle {\sqrt {x^{2}-4x}}<{\sqrt {10-x}}}$!

${\displaystyle {\sqrt {x^{2}-4x}}<{\sqrt {10-x}}}$

${\displaystyle ({\sqrt {x^{2}-4x}})^{2}<({\sqrt {10-x}})^{2}}$

${\displaystyle x^{2}-4x<10-x}$

${\displaystyle x^{2}-3x-10<0}$

dibuat harga nol

${\displaystyle x^{2}-3x-10=0}$

${\displaystyle (x+2)(x-5)=0}$

${\displaystyle x=-2\lor x=5}$

dibuat irisan

	-2		5
+++	N/A	----	N/A	+++

${\displaystyle -2<x<5}$

karena ada syarat akar maka:

akar 1

${\displaystyle x^{2}-4x\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-4x=0}$

${\displaystyle x(x-4)=0}$

${\displaystyle x=0\lor x=4}$

dibuat irisan

	0		4
+++	N/A	----	N/A	+++

${\displaystyle x\leq 0\lor x\geq 4}$

akar 2

${\displaystyle 10-x\geq 0}$

${\displaystyle x\leq 10}$

gabungkan umum dan syarat

irisan		-2		(0)		(4)		5		(10)
pertama	tidak	N/A	ya	N/A	ya	N/A	ya	N/A	tidak	N/A	tidak
kedua	ya	N/A	ya	N/A	tidak	N/A	ya	N/A	ya	N/A	ya
ketiga	ya	N/A	ya	N/A	ya	N/A	ya	N/A	ya	N/A	tidak

${\displaystyle HP=\{x|-2<x\leq 0\lor 4\leq x<5,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle {\sqrt {x^{2}-4}}\geq {\sqrt {3x+50}}}$!

${\displaystyle {\sqrt {x^{2}-4}}\geq {\sqrt {3x+50}}}$

${\displaystyle ({\sqrt {x^{2}-4}})^{2}\geq ({\sqrt {3x+50}})^{2}}$

${\displaystyle x^{2}-4\geq 3x+50}$

${\displaystyle x^{2}-3x-54\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-3x-54=0}$

${\displaystyle (x+6)(x-9)=0}$

${\displaystyle x=-6\lor x=9}$

dibuat irisan

	(-6)		(9)
+++	N/A	----	N/A	+++

${\displaystyle x\leq -6\lor x\geq 9}$

karena ada syarat akar maka:

akar 1

${\displaystyle x^{2}-4\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-4=0}$

${\displaystyle (x+2)(x-2)=0}$

${\displaystyle x=-2\lor x=2}$

dibuat irisan

	(-2)		(2)
+++	N/A	----	N/A	+++

${\displaystyle x\leq -2\lor x\geq 2}$

akar 2

${\displaystyle 3x+50\geq 0}$

${\displaystyle x\geq -{\frac {50}{3}}}$

gabungkan umum dan syarat

irisan		(-50/3)		(-6)		(-2)		(2)		(9)
pertama	ya	N/A	ya	N/A	tidak	N/A	tidak	N/A	tidak	N/A	ya
kedua	ya	N/A	ya	N/A	ya	N/A	tidak	N/A	ya	N/A	ya
ketiga	tidak	N/A	ya	N/A	ya	N/A	ya	N/A	ya	N/A	ya

${\displaystyle HP=\{x|2<x\leq 0\lor 4\leq x<5,x\in R\}}$

Pertidaksamaan Pecahan

Dalam bentuk pertidaksamaan pecahan sebagai berikut:

${\displaystyle {\frac {f(x)}{g(x)}}<0}$ atau ${\displaystyle {\frac {f(x)}{g(x)}}>0}$

haruslah mempunyai syarat yaitu penyebut atau g(x) ≠ 0.

• Tentukan nilai x dari pertidaksamaan ${\displaystyle {\frac {x-4}{x-3}}<{\frac {x+1}{x-2}}}$!

${\displaystyle {\frac {x-4}{x-3}}<{\frac {x+1}{x-2}}}$

${\displaystyle {\frac {x-4}{x-3}}-{\frac {x+1}{x-2}}<0}$

${\displaystyle {\frac {(x-4)(x-2)-(x+1)(x-3)}{(x-3)(x-2)}}<0}$

${\displaystyle {\frac {(x^{2}-6x+8)-(x^{2}-2x-3)}{(x-3)(x-2)}}<0}$

${\displaystyle {\frac {-4x+11}{(x-3)(x-2)}}<0}$

${\displaystyle -4x+11<0}$

${\displaystyle x<{\frac {11}{4}}}$

karena ada syarat pecahan maka:

penyebut 1

${\displaystyle x-3\neq 0}$

${\displaystyle x\neq 3}$

penyebut 2

${\displaystyle x-2\neq 0}$

${\displaystyle x\neq 2}$

dibuat irisan

	2		11/4		3
+++	N/A	----	N/A	+++	N/A	----

${\displaystyle HP=\{x|2<x<{\frac {11}{4}}\lor x>3,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle {\frac {x+6}{x+17}}\geq {\frac {1}{x-3}}}$!

${\displaystyle {\frac {x+6}{x+17}}\geq {\frac {1}{x-3}}}$

${\displaystyle {\frac {x+6}{x+17}}-{\frac {1}{x-3}}\geq 0}$

${\displaystyle {\frac {(x+6)(x-3)-(x+17)}{(x+17)(x-3)}}\geq 0}$

${\displaystyle {\frac {x^{2}+3x-18-x-17}{(x+17)(x-3)}}\geq 0}$

${\displaystyle {\frac {x^{2}+2x-35}{(x-3)(x-2)}}\geq 0}$

${\displaystyle x^{2}+2x-35\geq 0}$

dibuat harga nol

${\displaystyle x^{2}+2x-35=0}$

${\displaystyle (x+7)(x-5)=0}$

${\displaystyle x=-7\lor x=5}$ (tanpa gambar irisan)

karena ada syarat pecahan maka:

penyebut 1

${\displaystyle x+17\neq 0}$

${\displaystyle x\neq -17}$

penyebut 2

${\displaystyle x-3\neq 0}$

${\displaystyle x\neq 3}$

dibuat irisan

	-17		(-7)		3		(5)
+++	N/A	----	N/A	+++	N/A	----	N/A	+++

${\displaystyle HP=\{x|x<-17\lor -7\leq x<3\lor x\geq 5,x\in R\}}$

Pertidaksamaan Mutlak

Dalam bentuk pertidaksamaan mutlak sebagai berikut:

${\displaystyle |f(x)|<g(x)}$ atau ${\displaystyle |f(x)|>g(x)}$

haruslah mempunyai dua nilai yaitu

${\displaystyle |f(x)|=\left\{{\begin{matrix}|f(x)|<g(x),&{\mbox{maka penyelesaian}}-g(x)<f(x)<g(x)\\\\|f(x)|>g(x),&{\mbox{maka penyelesaian}}f(x)<-g(x)\lor f(x)>g(x)\end{matrix}}\right.}$

Pertidaksamaan mutlak akan memungkinkan definit + dan - karena tidak memotong dan menyinggung sumbu y.

• Tentukan nilai x dari pertidaksamaan ${\displaystyle |x^{2}+x|<12}$!

${\displaystyle |x^{2}+x|<12}$

karena f(x) < g(x) maka penyelesaian -g(x) < f(x) < g(x)

${\displaystyle -12<x^{2}+x<12}$

untuk ${\displaystyle -12<x^{2}+x}$

${\displaystyle -12<x^{2}+x}$

${\displaystyle x^{2}+x+12>0}$ definit +

untuk ${\displaystyle x^{2}+x<12}$

${\displaystyle x^{2}+x<12}$

${\displaystyle x^{2}+x-12<0}$

dibuat harga nol

${\displaystyle x^{2}+x-12=0}$

${\displaystyle (x+4)(x-3)<0}$

${\displaystyle x=-4\lor x=3}$

dibuat irisan

	-4		3
+++	N/A	----	N/A	+++

${\displaystyle -4<x<3}$

${\displaystyle HP=\{x|-4<x<3,x\in R\}}$

• Tentukan nilai x dari persamaan ${\displaystyle |x^{2}-4x-12|-|7-6x|\geq 5}$!

terlebih dahulu untuk mempunyai batas-batas yang ada

untuk | x^2 - 4x - 12 |

${\displaystyle |x^{2}-4x-12|=\left\{{\begin{matrix}x^{2}-4x-12,&{\mbox{maka penyelesaian}}x^{2}-4x-12\geq 0\\\\-(x^{2}-4x-12),&{\mbox{maka penyelesaian}}x^{2}-4x-12<0\end{matrix}}\right.}$

batasan f(x)

${\displaystyle x^{2}-4x-12\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-4x-12=0}$

${\displaystyle (x+2)(x-6)=0}$

${\displaystyle x=-2\lor x=6}$

dibuat irisan

	-2		6
+++	N/A	----	N/A	+++

${\displaystyle x\leq -2\lor x\geq 6}$

batasan -f(x)

${\displaystyle x^{2}-4x-12<0}$

dibuat harga nol

${\displaystyle x^{2}-4x-12=0}$

${\displaystyle (x+2)(x-6)=0}$

${\displaystyle x=-2\lor x=6}$

dibuat irisan

	-2		6
+++	N/A	----	N/A	+++

${\displaystyle -2<x<6}$

untuk | 7 - 6x |

${\displaystyle |7-6x|=\left\{{\begin{matrix}7-6x,&{\mbox{maka penyelesaian}}7-6x\geq 0\\\\-(7-6x),&{\mbox{maka penyelesaian}}7-6x<0\end{matrix}}\right.}$

batasan f(x)

${\displaystyle 7-6x\geq 0}$

${\displaystyle x\leq {\frac {7}{6}}}$

batasan -f(x)

${\displaystyle 7-6x<0}$

${\displaystyle x>{\frac {7}{6}}}$

keempat batas-batas akan dibuat irisan

irisan		-2		7/6		6
pertama	x^2 - 4x - 12	N/A		N/A		N/A	x^2 - 4x - 12
kedua		N/A	-(x^2 - 4x - 12)	N/A	-(x^2 - 4x - 12)	N/A
ketiga	7 - 6x	N/A	7 - 6x	N/A		N/A
keempat		N/A		N/A	-(7 - 6x)	N/A	-(7 - 6x)

untuk x <= -2

${\displaystyle x^{2}-4x-12-(7-6x)\geq 5}$

${\displaystyle x^{2}-4x-12-7+6x-5\geq 0}$

${\displaystyle x^{2}+2x-24\geq 0}$

dibuat harga nol

${\displaystyle x^{2}+2x-24=0}$

${\displaystyle (x+6)(x-4)=0}$

${\displaystyle x=-6\lor x=4}$

dibuat irisan

	(-6)		(-2)		(4)
Ya	N/A	Ya	N/A	Tidak	N/A	Tidak
+++	N/A	----	N/A	----	N/A	+++

${\displaystyle x\leq -6}$

untuk -2 < x <= 7/6

${\displaystyle -(x^{2}-4x-12)-(7-6x)\geq 5}$

${\displaystyle -x^{2}+4x+12-7+6x-5\geq 0}$

${\displaystyle x^{2}-10x\leq 0}$

dibuat harga nol

${\displaystyle x^{2}-10x=0}$

${\displaystyle x(x-10)=0}$

${\displaystyle x=0\lor x=10}$

dibuat irisan

	-2		(0)		(7/6)		(10)
Tidak	N/A	Ya	N/A	Ya	N/A	Tidak	N/A	Tidak
+++	N/A	+++	N/A	----	N/A	----	N/A	+++

${\displaystyle 0\leq x\leq {\frac {7}{6}}}$

untuk 7/6 < x < 6

${\displaystyle -(x^{2}-4x-12)-(-(7-6x))\geq 5}$

${\displaystyle -x^{2}+4x+12+7-6x-5\geq 0}$

${\displaystyle x^{2}+2x\leq 0}$

dibuat harga nol

${\displaystyle x^{2}+2x=0}$

${\displaystyle x(x+2)=0}$

${\displaystyle x=0\lor x=-2}$

dibuat irisan

	(-2)		(0)		7/6		6
Tidak	N/A	Tidak	N/A	Tidak	N/A	Ya	N/A	Tidak
+++	N/A	----	N/A	+++	N/A	+++	N/A	+++

${\displaystyle \varnothing }$

untuk x >= 6

${\displaystyle x^{2}-4x-12-(-(7-6x))\geq 5}$

${\displaystyle x^{2}-4x-12+7-6x-5\geq 0}$

${\displaystyle x^{2}-10x-10\geq 0}$ definit +

${\displaystyle \varnothing }$

${\displaystyle HP=\{x|x\leq -6\lor 0\leq x\leq {\frac {7}{6}},x\in R\}}$

gabungkan ketiga batas-batas. jadi:

${\displaystyle HP=\{x|-{\frac {11}{5}}\leq x<-{\frac {4}{3}}\lor -{\frac {4}{3}}\leq x\leq 3,x\in R\}}$

${\displaystyle HP=\{x|-{\frac {11}{5}}\leq x\leq 3,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle |{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|}$!

${\displaystyle |{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|}$

${\displaystyle ({\frac {x+4}{10-x}})^{2}<({\frac {1}{x-2}})^{2}}$

${\displaystyle ({\frac {x+4}{10-x}})^{2}-({\frac {1}{x-2}})^{2}<0}$

${\displaystyle ({\frac {x+4}{10-x}}+{\frac {1}{x-2}})({\frac {x+4}{10-x}}-{\frac {1}{x-2}})<0}$

${\displaystyle ({\frac {(x+4)(x-2)+10-x}{(10-x)(x-2)}})({\frac {(x+4)(x-2)-(10-x)}{(10-x)(x-2)}})<0}$

${\displaystyle ({\frac {x^{2}+2x-8+10-x}{(10-x)(x-2)}})({\frac {x^{2}+2x-8-10+x}{(10-x)(x-2)}})<0}$

${\displaystyle ({\frac {x^{2}+x+2}{(10-x)(x-2)}})({\frac {x^{2}+3x-18}{(10-x)(x-2)}})<0}$

akar dari ${\displaystyle {\frac {x^{2}+x+2}{(10-x)(x-2)}}}$

${\displaystyle {\frac {x^{2}+x+2}{(10-x)(x-2)}}<0}$

${\displaystyle x^{2}+x+2=0}$ definit +

karena ada syarat pecahan maka:

penyebut 1

${\displaystyle 10-x\neq 0}$

${\displaystyle x\neq 10}$

penyebut 2

${\displaystyle x-2\neq 0}$

${\displaystyle x\neq 2}$

akar dari ${\displaystyle {\frac {x^{2}+3x-18}{(10-x)(x-2)}}}$

${\displaystyle {\frac {x^{2}+3x-18}{(10-x)(x-2)}}<0}$

${\displaystyle x^{2}+3x-18<0}$

dibuat harga nol

${\displaystyle x^{2}+3x-18=0}$

${\displaystyle (x+6)(x-3)=0}$

${\displaystyle x=-6\lor x=3}$ (tanpa gambar irisan)

karena ada syarat pecahan maka:

penyebut 1

${\displaystyle 10-x\neq 0}$

${\displaystyle x\neq 10}$

penyebut 2

${\displaystyle x-2\neq 0}$

${\displaystyle x\neq 2}$

dibuat irisan

	-6		2*		3		10*
+++	N/A	----	N/A	----	N/A	+++	N/A	+++

nb: * = mempunyai 2 akar

${\displaystyle HP=\{x|-6<x<3,x\in R\}}$

• Tentukan nilai x dari pertidaksamaan ${\displaystyle |{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|}$!

${\displaystyle |{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|}$

${\displaystyle ({\sqrt {x^{2}-4x}})^{2}\geq ({\sqrt {3x-10}})^{2}}$

${\displaystyle x^{2}-4x\geq 3x-10}$

${\displaystyle x^{2}-7x+10\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-7x+10=0}$

${\displaystyle (x-2)(x-5)=0}$

${\displaystyle x=2\lor x=5}$

dibuat irisan

	2		5
+++	N/A	----	N/A	+++

${\displaystyle x\leq 2\lor x\geq 5}$

karena ada syarat akar maka:

akar 1

${\displaystyle x^{2}-4x\geq 0}$

dibuat harga nol

${\displaystyle x^{2}-4x=0}$

${\displaystyle x(x-4)=0}$

${\displaystyle x=0\lor x=4}$

dibuat irisan

	0		4
+++	N/A	----	N/A	+++

${\displaystyle x\leq 0\lor x\geq 4}$

akar 2

${\displaystyle 3x-10\geq 0}$

${\displaystyle x\geq {\frac {10}{3}}}$

gabungkan umum dan syarat

irisan		(0)		(2)		(10/3)		(4)		(5)
pertama	ya	N/A	ya	N/A	tidak	N/A	tidak	N/A	tidak	N/A	ya
kedua	ya	N/A	tidak	N/A	tidak	N/A	tidak	N/A	ya	N/A	ya
ketiga	tidak	N/A	tidak	N/A	tidak	N/A	ya	N/A	ya	N/A	ya

${\displaystyle HP=\{x|x\geq 5,x\in R\}}$

	-2		5
+++	N/A	----	N/A	+++