Nama saya Dhea Damayanti R (201831007), Saya adalah salah satu mahasiswa di STT-PLN Jakarta.
Halaman Blog ini saya buat untuk tugas KALKULUS.
Halaman Blog ini saya buat untuk tugas KALKULUS.
"Turunan Fungsi"
Sekolah Tinggi Teknik PLN Jakarta
Turunan Fungsi
Pengertian Turunan
Turunan
adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan
nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana
suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam
menemukan turunan disebut diferensiasi.
Pada fungsi y = f(x), turunan dari variabel y terhadap variabel x dinotasikan dengan  atau
atau 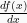 atau y’ dan didefinisikan sebagai:
atau y’ dan didefinisikan sebagai:
Rumus-rumus Turunan Fungsi Aljabar
Dengan definisi turunan akan dicari rumus-rumus turunan fungsi aljabar yang terdiri dari fungsi pangkat  , hasil kali fungsi f(x) = u(x) . v(x), hasil pembagian fungsi
, hasil kali fungsi f(x) = u(x) . v(x), hasil pembagian fungsi  , dan pangkat dari fungsi
, dan pangkat dari fungsi  .
.
1. Rumus turunan fungsi pangkat 
Fungsi berbentuk pangkat turunannya dapat menggunakan rumus 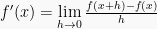 sebagai:
sebagai:
Jadi rumus turunan fungsi pangkat adalah:
2. Rumus turunan hasil kali fungsi 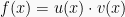
Fungsi f(x) yang terbentuk dari perkalian fungsi u(x) dan v(x), turunannya didapat dengan:
Jadi rumus turunan fungsinya adalah:
3. Rumus turunan fungsi pembagian 
sehingga
Jadi rumus turunan fungsinya adalah
4. Rumus turunan pangkat dari fungsi 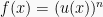
Ingat jika  , maka:
, maka:
Karena 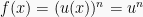 , maka:
, maka:
Atau
Jadi rumus turunan fungsinya adalah:

Tidak ada komentar:
Posting Komentar